Building a parser

Jul 11, 2024 | Reading time: 23 minutes

Write a lexical parser in Haskell

Haskell is widely used in academic stages and for teaching the functional programming paradigm. Consequently, there are numerous examples and implementations in Haskell for building parsers.

In this tutorial, I will describe the process of writing a simple parser in Haskell, with the dual purpose of learning Haskell and understanding how to write a parser. My intent is not to teach others how to do this kind of project in detail, as there are already many excellent tutorials and examples that I followed. Instead, I aim to offer a different point of view, focused on beginners in Haskell, like myself.

First of all, some concepts need to be understood before start writing.

What a Parser is

Parsers are software tools that read and analyze a stream of input and convert it into syntax structures. The input could be a String or a list of symbols. Parsers determine whether the input follows a Formal Grammar or not.

What a Formal Grammar is

Formal Grammar describes which strings from an alphabet are part of the language the grammar defines. A grammar is defined by a tuple with the alphabet (a set of indivisible terms), the production rules, the initial state, and the set of terminal states. They are represented as $(V, T, S, P)$ where:

$V$ is a finite set of non-terminal symbols
$T$ is a finite set of terminal symbols
$S$ is the initial state. Because that, should accomplish $S \in V \cup S \in T$
$P$ is a finite set of production rules, that $P_{i} (V_{k}) - > N_{j}, N \in V \cup T$
$V \cap T = \emptyset$

The production rules transform or substitute a Start symbol into another sequence of symbols. If the grammar can produce a string, we say that this string is part of the language, and it is valid. There exist different forms of grammar representation, but I will focus on the EBNF .

A symbol is a variable, that always is enclosed by a pair < >
$::=$ The symbol on the left should be replaced by the right part.
An expression is one or more sequences of symbols, where each sequence is separated by “|” which means or
${$ and $}$ means zero or more
$[$ and $]$ means zero or once

For example, a grammar that represents unsigned hexadecimal numbers can be described as:

G = (V, T, S, P)
V = { <hexdigit>, <hexnumber>, <digit>, <alpha> }
T = { '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'a', 'b', 'c', 'd', 'e', 'f' }
P = {
    S ::= <hexnumber>
    <hexnumber> ::= < hexnumber > <hexdigit >  | <hexdigit>
    <hexdigit> ::= <digit> | <alpha>
    <digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
    <alpha> ::= a | b | c | d | e | f
}

If you pay attention, you can see that the second production rule prefers to set the terminal symbol on the right and transform the left symbol. This is a special case of context-free grammar called left-linear. A grammar could be either left-linear or right-linear, but not both.

Following the EBNF notation, the following rules are equivalent:

<hexnumber> ::= <hexnumber> <hexdigit> | <hexdigit>
<hexnumber> ::= {<hexnumber>} <hexdigit>

Types of production rules
- Sequence: a symbol is transformed into a sequence of symbols $S ::= A B$
- Repetition: A symbol could appear zero or any times $S ::= {A} B$
- Optional: A symbol could appear zero or one time $S :: [A] B$

Abstract syntax tree

If the input is valid, the parser returns an Abstract syntax tree (AST). An AST is a tree representation of a sentence where each node can only be evaluated after its children have been evaluated. This means that the tree is read bottom up.

Example of AST with a simple mathematical operation

Let’s practice!

Setup the project

I use cabal to manage the project, but stack is also available. To initialize the project, execute

$ mkdir dummy-calc && cd $_ cabal init --interactive

The command will prompt you for some questions and create the folder structure with a result similar to the following one. I changed the name of the test main file from Main.hs to Spec.hs because I want to use Spec test suit library.

tree .
.
├── app
│   └── Main.hs
├── dummy-calc.cabal
├── CHANGELOG.md
├── LICENSE
├── src
│   └── DummyCalc.hs
└── test
    └── Spec.hs

4 directories, 6 files

In the file dummy-calc.cabal At the test-suit, on the test-suit, we should append. This configuration allows us to compile and run with multiples threads the tests and use the hspec-discover option to automatize the process.

ghc-options:
  -O -threaded -rtsopts -with-rtsopts=-N
build-tool-depends:
  hspec-discover:hspec-discover

Define the alphabet

As mentioned before, grammars are defined by an alphabet and a set of production rules. For the alphabet, I use a set of TOKENS. A token is the smallest unit of information in the language that we are designing. At this point, our dummy calc only recognizes the simplest math expression (+, -, *, /) and parenthesis to determine the priority of the operations. But, at some point, I want to allow other operations such as assigning a value to a variable.

We will create a file, named Tokens.hs in the folder src/DummyCalc/Calc/Lexer/ and use a Data constructor to define them.

The Data keyword allows for defining new data structures. We are wrapping a set of newtype into a new Data type. So, when a function signature specifies the Data type created, it could be any of the new types that are defined within it. You can think of them as a combination of both, structs and enums. In haskell this declaration is known as algebraic data types.

The data declaration looks like:

data <Type-Name> <type-args>
  = <Data-Constructor1> <types>
  = <Data-Constructor2> <types>

The advantages from the data declaration versus the newtype are:

We can write many types in the <types> part, not only one.
We can have alternative structures using the or operator |

Into the file src/DummyCalc/Lexer/Tokens.hs we can define the tokens as:

-- | Token are the smallest semantically piece of information.
-- | Each constructor represent an abstraction of the readed text
-- | except TokOperator and TokNumber which need information about the values
-- | they represent
data Token
  = TokLeftParen -- ^ (
  | TokRightParen -- ^ )
  | TokEquals -- ^ =
  | TokOperator La.Operation -- ^ + | - | * | /
  | TokNumber La.NumValue -- ^ a number
  | TokVar La.Variable -- ^ a variable
  | TokEof -- ^ End Of File
  | TokEos -- ^ End of Sentence
  | TokError String-- ^ Error
  deriving (Eq)

In Haskell, we can extend a custom type with the properties of other classes. For example, in the example above, We are extending, or deriving the class Eq which offers the method (==). This method returns True if both parameters are equal. This means that our Tokens can be compared between them. If we need more control over the method that the class provides, we can define an instance of a type class manually.

instance Show Token where
  show TokLeftParen  = "'('"
  show TokRightParen = "')'"
  show TokEquals     = "'='"
  show (TokOperator op) = show op
  show (TokNumber v) = "TN " <> (show v)
  show (TokVar v)    = show v
  show TokEof        = "EOF"
  show TokEos        = "EOS"
  show (TokError char) = "Unrecogniced token at " <> char

In this case, we are applying something similar to the polymorphism in POO. Now, when we call the function show with and argument of type Token, the function that will be called will be one of the defined above, depending on the element that have to be showed.

Lexical Analysis

Once we have defined all the data structures, we need to read an input and convert it into these structures. This process is known as lexical analysis and can be defined as the process of reading a text and assembling it into a sequence of lexemes or tokens.

We can make a function that reads the string and returns a list of Token. This function is written in the file src/DummyCalc/Calc/Lexer.hs

-- | Convert a string into a list of lexems
lexer :: String -> [Token]
lexer "" = []
lexer xs@(x:xs')
  | isSpace x = lexer xs'
  | x == '(' = TokLeftParen : lexer xs'
  | x == ')' = TokRightParen : lexer xs'
  | x == '=' = caseEquals xs'
  | x == ';' = caseIsEndOfFile xs' -- TokEos : lexer xs'
  | isDigit x = caseReadValue xs
  | isOpChar x = caseReadOperator xs
  | isValidAsFirstChar x = caseIsVariable xs
  | otherwise = TokError [x] : lexer xs'

Code Snippet 1: lexer definition

This is a recursive function that reads character by character the input, and has contemplated the following case:

Base Case. If the input is empty, the function returns an empty list.
If the input is a space, the function returns the result of executing the function skipping this character.
Prepend a Left or Right parenthesis to the result of the next execution (Read the next character).
Evaluate if the character is a digit, an operation, or an error, then prepend the corresponding Token to the result of the next execution.

This is a good example of how the language works. The lexer function is implemented following:

pattern match on the argument. It means, decide which operation execute based on some specifications of the argument. In this case, we are checking if the string is empty with the lexer "" = [] rule, or if it has almost one element lexer (x:xs)
The as (@) operator which allows us to assign a name to a pattern for its use on the right-hand. So with xs@(x:xs'), we are define xs as the whole input, x as the first character (the head) and xs' as the rest of the input (the tail).
Guards that acts like if elif else in other languages. Note that when we are defining a function with guards, we do not use the equal sign after the definition, instead, we use the equal sign after each condition.

The function defined in the listing 1 , use some helpers function. isSpace and isDigit are defined in Data.Char. In case, the character at this point is a digit, the token value is evaluated with the functions readValue, and stringToDouble (listing 2 ). isOpChar is defined in src/DummyCalc/Lexer/Tokens.hs (listing 3 )

-- | Read a string and returns the number at this position and the remaining
-- | text or an SyntaxError in case of invalid number
stringToDouble :: String -> Either SyntaxError (Double, String)
stringToDouble ('-':xs) = case stringToDouble xs of
                           Right (v, rest) -> Right (-v, rest)
                           Left _ -> Left InvalidNumber
stringToDouble xs'@('.':_) = stringToDouble $ '0':xs'
stringToDouble xs@(x:_)
  | isDigit x = Right (read digitPart :: Double, restPart)
  | otherwise = Left InvalidNumber
  where (digitPart, restPart) = span (\c -> isDigit c  || c == '.') xs
stringToDouble "" = Left InvalidNumber

readValue :: String -> Either SyntaxError (NumValue, String)
readValue xs = case stringToDouble xs of
                     Right (value, left) -> Right (NumValue value, left)
                     Left l -> Left l

Code Snippet 2: readValue converts an string into a value using the function string to double

-- | A list with valid character that composes the operations
opChars :: String
opChars = "+-*/~<=>!&|%^"

-- | Function that returns wheter a character is an operation character or not
isOpChar :: Char -> Bool
isOpChar x = x `elem` opChars

-- | Function that, given a String, returns the correspondent Operation
stringToOperator :: String -> Maybe La.Operation
stringToOperator "+" = Just La.Summatory
stringToOperator "-" = Just La.Difference
stringToOperator "*" = Just La.Multiplication
stringToOperator "/" = Just La.Division
stringToOperator _ = Nothing

-- | Read the character at the current position, and returns the right part,
-- | (La.Operation, String) Tuple, if success, and the left part, an SyntaxError, otherwise
readOperator :: String -> Either SyntaxError (La.Operation, String)
readOperator xs = case stringToOperator op of
                    Just o -> Right (o, rest)
                    Nothing -> Left InvalidOperator
                  where
                    (op, rest) = span isOpChar xs

Code Snippet 3: isOpChar checks if the character at point is a valid operation, and if it is the case, convert them to an operation representation

Test Suit

Now we have a function that read a String as input and returns a list of Tokens, but we need to test it. To write the test suit, I use the hspec library. This library or framework, allows automatic test discover. This library, get a list of modules that contain tests and execute them, following the TDD principle. This practice help us to be sure our code works fine.

We need to test dependencies, so on the test-suit of the cabal file, you should have something like:

build-depends:
    base ^>=4.17.2.1
  , dummy-calc
  , hspec
  , hspec-discover
  , raw-strings-qq

And add the modules where the tests will be written

-- Modules included in this executable, other than Main.
other-modules:
    LexerSpec
    ParserSpec
    EvalSpec

With all of them, we add the following instruction to invoke the hspec-discover in the test/Spec.hs file

{-# OPTIONS_GHC -F -pgmF hspec-discover #-}

Test the lexer function

Once we set up the test suit, we can write our first tests in the file test/LexerSpec.hs. Remember that all the modules have to end with “Spec” to be discovered.

module LexerSpec where
import Test.Hspec

import qualified DummyCalc.Lexer as Lexer
import qualified DummyCalc.Lexer.Tokens as Token
import DummyCalc.Language as La

spec :: Spec
spec = do
  describe "Test the lexer function" $ do
    it "Test (5+9)" $
      shouldBe (Lexer.lexer "(5+9)")
               [ Token.TokLeftParen
               , Token.TokNumber $ La.NumValue 5
               , Token.TokOperator $ La.Summatory
               , Token.TokNumber $ La.NumValue 9
               , Token.TokRightParen
               ]
    it "Test 5 + 9" $
      shouldBe (Lexer.lexer "5 + 9")
               [ Token.TokNumber $ La.NumValue 5
               , Token.TokOperator $ La.Summatory
               , Token.TokNumber $ La.NumValue 9
               ]
    it "Test 5 + -9" $
      shouldBe (Lexer.lexer "5 + -9")
               [ Token.TokNumber $ La.NumValue 5
               , Token.TokOperator $ La.Summatory
               , Token.TokOperator $ La.Difference
               , Token.TokNumber $ La.NumValue 9
               ]
    it "Test 7*9/3" $
      shouldBe (Lexer.lexer "7*9/3")
               [ Token.TokNumber $ La.NumValue 7
               , Token.TokOperator $ La.Multiplication
               , Token.TokNumber $ La.NumValue 9
               , Token.TokOperator $ La.Division
               , Token.TokNumber $ La.NumValue 3
               ]
    it "Test let x => 5" $
      shouldBe
        (Lexer.lexer "x => 5")
        [ Token.TokVar $ La.Variable "x"
        , Token.TokEquals
        , Token.TokNumber $ La.NumValue 5
        ]
    it "Test x*9" $
      shouldBe
        ( Lexer.lexer "x*9")
        [ Token.TokVar $ La.Variable "x"
        , Token.TokOperator $ La.Multiplication
        , Token.TokNumber $ La.NumValue 9
        ]
    it "Test x*(9-8)/3+2" $
      shouldBe
        ( Lexer.lexer "x*(9-8)/3+2")
        [ Token.TokVar $ La.Variable "x"
        , Token.TokOperator La.Multiplication
        , Token.TokLeftParen
        , Token.TokNumber $ La.NumValue 9
        , Token.TokOperator La.Difference
        , Token.TokNumber $ La.NumValue 8
        , Token.TokRightParen
        , Token.TokOperator La.Division
        , Token.TokNumber $ La.NumValue 3
        , Token.TokOperator La.Summatory
        , Token.TokNumber $ La.NumValue 2
        ]
    it "Test x=>5;x+3" $
      shouldBe
        ( Lexer.lexer "x=>5;x+3")
        [ Token.TokVar $ La.Variable "x"
        , Token.TokEquals
        , Token.TokNumber $ La.NumValue 5
        , Token.TokEos
        , Token.TokVar $ La.Variable "x"
        , Token.TokOperator La.Summatory
        , Token.TokNumber $ La.NumValue 3
        ]

Define the language symbols.

In the lexical analysis we define the Token list as a small piece of information. But some of the constructors of the data type requires more information. For example, the operator and the numbers. Both could be represented as Char/String or a Double, but if we define a Language module, will be easier extends it latter. The Language module is imported with the qualified import as DummyCalc.Language as La. This module, only exports the Value and the Operation constructors, but both are defined in DummyCalc.Language.Data.Internal

module DummyCalc.Language
  ( Value
  , NumValue(..)
  , Operation(..)
  , ValType(..)
  , Variable(..)
  ) where

import DummyCalc.Language.Data.Operations
import DummyCalc.Language.Data.Types

And the types are defined as:

module DummyCalc.Language.Data.Operations where

-- | A Data type to store the valid opertions
data Operation
  = Summatory
  | Difference
  | Multiplication
  | Division
  | Assign

instance Show Operation where
  show op = case op of
    Summatory       -> "ADD"
    Difference      -> "SUB"
    Multiplication  -> "MUL"
    Division        -> "DIV"
    Assign          -> "ASS"

instance Eq Operation where
  (==) Summatory Summatory            = True
  (==) Difference Difference          = True
  (==) Multiplication Multiplication  = True
  (==) Division Division              = True
  (==) Assign Assign                  = True
  (==) _ _                            = False


data Variable

As you can see, our Value only has one constructor, so we can use newtype instead of data, But the process is the same.

At the code-block above, we can see two ways of extends a class, the first one is using the case of operator, which works like a switch. When the op matches with one of the options, the function returns the right part of the evaluation. The part that are after the arrow. On the other hand, the second extensions works in the same way we see above in

Write the parser

At this point, we have the lexer program, that convert a string input into a list of valid tokens, and an abstraction of the types that our language could manage. Now we need to convert the tokens into the AST. To make that, we will use a recursive descent parsing

The recursive descent parser is an approach that could be used to parser languages with relatively simple grammar. It is a top-down parser, a type of parser that begins with a Start symbol and try to determine the parser tree by working down the levels. By contrast, a bottom-up parser, first recognizes the low-level syntactic units and build the parser from these towards the root.

For our dummy calc we can represent the syntax trees using algebraic data types.

Using the implementation in 42 Abstract Syntax Tree , with a few modifications

type StatementList = [Statement]

data Program = Program StatementList deriving (Show, Eq)
data Statement
  = Statement Expr
  | Ass La.Variable Expr
  deriving (Show, Eq)

data EOF = EOF deriving (Show, Eq)
data EOS = EOS deriving (Show, Eq)

data Expr
  = Add Expr Expr
  | Sub Expr Expr
  | Mul Expr Expr
  | Div Expr Expr
  | Var La.Variable
  | Val La.Value
  deriving (Eq)

In the block , we are defining a basic set of rules, for example, that a program is a Statement list. A Statement is either an Statement followed by an Expression, or an assignation. EOF and EOS correspond with End of File and End of Sentence respectively and different types of Expressions.

At the same time, we could need some way to display or represent as String this kind of structures, so we can extend the Show class with our custom data types.

instance Show Expr where
  show (Val v) = show v
  show (Var n) = show n
  show (Add l r) = showPar "+" l r
  show (Sub l r) = showPar "-" l r
  show (Mul l r) = showPar "*" l r
  show (Div l r) = showPar "/" l r

showPar :: String -> Expr -> Expr -> String
-- showPar o e1 e2 = "(" <> show e1 <> " " <> o <> " " <> show e2 <> ")"
showPar o e1 e2 = "(" <> o <> " " <> show e1 <> " " <> show e2 <> " )"

Finally, we need to handle the possible errors from the input our language is reading.

data ParErr
  = MissingAddOp [Token]
  | MissingMulOp [Token]
  | MissingValue [Token]
  | MissingLeftParen [Token]
  | MissingRightParen [Token]
  | MissingEndOfFile [Token]
  | InvalidAssignExpression [Token]
  | MissingSemiColon     Statement [Token]
  | MissingFactor        ParErr [Token] Int
  | MissingStatementList ParErr [Token] Int
  | InvalidProgram       ParErr [Token] Int
  | NotImplemented String
  deriving (Eq)

instance Show ParErr where
  show (MissingAddOp xs) =
    "MissingAddOp: Missing add-like operator at \"" <> show (takeTokens xs) <> "\""
  show (MissingMulOp xs) =
    "MissingMulOp: Missing mul-like operator at \"" <> show (takeTokens xs) <> "\""
  show (MissingFactor err xs l) =
    "MissingFactor: Missing value or parenthesized expression beginning at \"" <> show
    (takeTokens xs) <> "\" with nested error \n" <> (replicate l '\t') <>
    "[" <> show err <> "]"
  show (MissingValue xs) =
    "MissingValue: Missing value at \"" <> show (takeTokens xs) <> "\""
  show (MissingLeftParen xs) =
    "MissingLeftParen: Missing '(' at \"" <> show (takeTokens xs) <> "\""
  show (MissingRightParen xs) =
    "MissingRightParen: Missing ')' at \"" <> show (takeTokens xs) <> "\""
  show (MissingEndOfFile xs) =
    "MissingEndOfFile: Missing EOF character at \"" <> show (takeTokens xs) <> "\""
  show (MissingStatementList e xs l) =
    "MissingStatementList: Missing statement list at \"" <> show (takeTokens xs) <>
    "\" with nested error \n" <> (replicate l '\t') <> show e
  show (InvalidProgram err xs l) =
    "InvalidProgram: Invalid program expression at \"" <> show (takeTokens xs) <>
    "\" with nested error \n" <> (replicate l '\t') <> show err <> "]"
  show (MissingSemiColon e xs) =
    "MissingSemiColon: Missing semicolon in Statement" <> show e <>
    " at \"" <> show (takeTokens xs) <> "\""
  show (InvalidAssignExpression xs) =
    "InvalidAssignExpression: Invalid assign expression at \"" <> show (takeTokens xs) <> "\""
  show (NotImplemented f) = "Function: " <> f <> " is not implemented"

Each node has an operator and two sides, that are other Expression. With this representation, we can build any operation and keep the priorities.

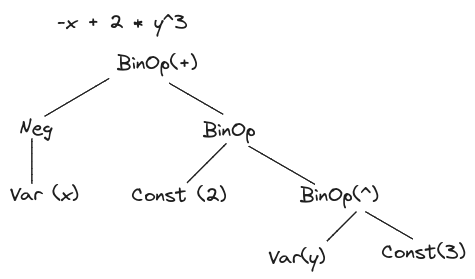
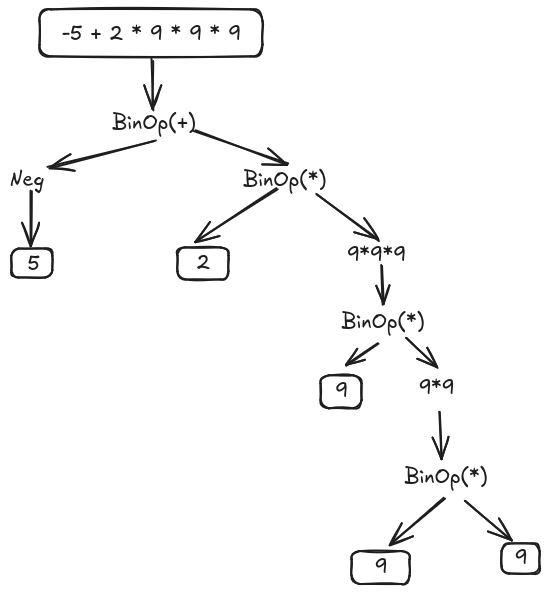
For example, in the AST image, we have the operation $- x + 2 * y^{3}$ . We did not implemented the pow operator or the use of variables, so we will replace the $x = 5$ and the $y = 9$ . Also, the pow operation, will be replaced by $y * y * y)$ . Now, we have the expression $- 5 + 2 * 9 * 9 * 9$ . This expression is equivalent to $(+ (- 5) (* (* (* 2 9) 9) 9))$ . As a AST, it is represent as:

represent the AST for the operation -5 + 2 * 9 * 9 * 9

Rules

When we describe the grammars, we define 3 types of production rules, sequence, repetition and optional. So, with this in mind, we need to design the formal grammar used to parse the input and transform it into an AST. It is important to remember that we need to keep the order of the priorities, and the associative and distribute properties. It is not the same $5 - 3 + 2 \neq 5 - (3 + 2)$ or $5 - 3 * 2 \neq (5 - 3) * 2$ . To ensure this, we will move down the multiplication and division operation, and keep up the sum and difference.

Note For portability, I will use uppercase for non-terminal symbols, and lowercase in other case.

Table 1: table with the rules of the grammar

Rule	Left side	Right side
0	S	EXPRESSION
1	EXPRESSION	TERM { MORETERMS }
2	TERM	FACTOR { MOREFACTORS }
3	FACTOR	val or NESTEXPRESSION
4	MORETERMS	ADDOP TERMINAL
5	MOREFACTOR	MULOP FACTOR
6	ADDOP	+ or -
7	MULOP	* or /
8	NESTEXPRESSION	( EXPRESSION )

In Haskell, each rule can be a function that reads the current token, and returns a tuple with an Expression and the rest of tokens. The functions can be categorize based on the type of rule they are represented.

S  ::= E
E  ::= T  U' -- Sequence
U' ::= { U } -- zero or more ocurrence
T  ::= F  G'
G' ::= { G }
-- F  ::= [ '-' ] n | l E r -- Alternative and opcional
F  ::= D | N
D  ::= ['-'] n
N  ::= l E r
U  ::= ('+' | '-') T
G  &::= ('*' | '/') F

The rule 1 in table 1 , can be refactor into the equation . Now we have tree rules, all of them match only one of the rules pattern described previously. The implementation, is in the file src/DummyCalc/Parser.hs and can be show in listing 4 . The same can be apply with the terms as show the equation and in the listing 5

expression ::=  term moreTerms
moreTerms  ::=  { addterm }
addterm    ::= addop term

parseExpression :: [Token] -> (Either ParErr Expr, [Token])
parseExpression xs =
  case parseTerm xs of
    (Right t1, ys) ->
      let (terms, zs) = parseMoreTerms ys
      in  (Right (makeBinOpSeq t1 terms), zs)
    (err@(Left _), _) -> (err, xs)

-- Repetition: <moreterms> ::= { <addterm> }
parseMoreTerms :: [Token] -> ([AddTerm], [Token])
parseMoreTerms xs =
  case parseAddTerm xs of
    (Right (op,ex), ys) ->
      let (terms, zs) = parseMoreTerms ys
      in ((op,ex):terms,zs)
    (Left _, _) -> ([], xs)

-- Sequence <addterm> ::= <addop> <term>
parseAddTerm :: [Token] -> (Either ParErr AddTerm, [Token])
parseAddTerm xs'@((TokOperator op):xs)
  | isAddOp op = case parseTerm xs of
                   (Right ex, zs) -> (Right (op,ex), zs)
                   (Left err, _) -> (Left err, xs')
parseAddTerm xs' = (Left $ MissingAddOp xs', xs')

isAddOp :: La.Operation -> Bool
isAddOp La.Summatory = True
isAddOp La.Difference = True
isAddOp _ = False

Code Snippet 4: parse expression

term        ::= factor moreFactors
moreFactors ::= { mulFactor }
mulFactor   ::= mulOp factor

parseTerm :: [Token] -> (Either ParErr Expr, [Token])
parseTerm xs =
  case parseFactor xs of
    (Right f1, ys) ->
     let (factors, zs) = parseMoreFactors ys
     in  (Right (makeBinOpSeq f1 factors), zs)
    (err@(Left _), _) -> (err, xs)


parseMoreFactors :: [Token] -> ([MulFactor], [Token])
parseMoreFactors xs =
  case parseMulFactor xs of
    (Right (op,ex), ys) ->
      let (factors, zs) = parseMoreFactors ys
      in  ((op,ex):factors, zs)
    (Left _, _) -> ([], xs)

parseMulFactor :: [Token] -> (Either ParErr MulFactor, [Token])
parseMulFactor ((TokOperator op):xs)
  | isMulOp op = case parseFactor xs of
                   (Right ex, zs) -> (Right (op, ex), zs)
                   (Left err, _)  -> (Left err, xs)
parseMulFactor xs = (Left $ MissingMulOp xs, xs)

isMulOp :: La.Operation -> Bool
isMulOp La.Multiplication = True
isMulOp La.Division = True
isMulOp _ = False

Code Snippet 5: parse terms

The rule 3, that apply to a factor, has 2 options. Convert the factor into a value, or into a nest expression. This case can be represented a try/catch where first try to convert into a value, if the program fails, then try to convert into a nest expression. The implementation is something similar to listing 6 , where each option has its own function.

parseFactor :: [Token] -> (Either ParErr Expr, [Token])
parseFactor xs =
  case parseVar xs of
    r@(Right _, _) -> r
    _ ->
      case parseVal xs of
        r@(Right _, _) -> r
        _ ->
          case parseNestExpr xs of
            r@(Right _, _) -> r
            (Left m, ts) -> (Left $ MissingFactor m ts 0, ts)


parseVal :: [Token] -> (Either ParErr Expr, [Token])
parseVal ((TokNumber n):xs) = (Right (Val n), xs)
parseVal ((TokOperator La.Difference):(TokNumber (La.NumValue n)):xs) =
  (Right $ Val $ La.NumValue (-n), xs)
parseVal xs = (Left $ MissingValue xs, xs)

parseVar :: [Token] -> (Either ParErr Expr, [Token])
parseVar ((TokVar x):xs) = (Right (Var x), xs)
parseVar xs = (Left $ NotImplemented "parseVar", xs)

-- | <nestexpr> ::= ( <expr> )
parseNestExpr :: [Token] -> (Either ParErr Expr, [Token])
parseNestExpr xs@(TokLeftParen:ys) =
  case parseExpression ys of
    (ex@(Right _), zs) ->
      case zs of
        (TokRightParen:as) -> (ex,as)
        _                  -> (Left $ MissingRightParen zs, xs)
    (err@(Left _), _) -> (err, xs)
parseNestExpr xs = (Left $ MissingLeftParen xs, xs)

Code Snippet 6: parse factors

The final grammar looks like:

S  &::= E
E  &::= T  U' -- Sequence
U' &::= { U } -- zero or more ocurrence
T  &::= F  G'
G' &::= { G }
-- F  &::= [ '-' ] n | l E r -- Alternative and opcional
F  &::= D | N
D  &::= ['-'] n
N  &::= l E r
U  &::= ('+' | '-') T
G  &::= ('*' | '/') F

Combining the expression

The final step is to combine expressions into operations. Since we are only working with binary operations, we need to combine two expressions at a time using the previously defined operator. The expressions must be combined from left to right. Therefore we begin with an initial expression and a list of pairs, each containing an operator and an expression. The result is a new expression, as shown in src/DummyCalc/Parser/AST.hs.

-- | Shortcut for the header 2 expressions as parameters and returns a new one.
type Constructor = Expr -> Expr -> Expr

{- |
Given an initial expression, and a list of tuples with operators and expression,
returns a new expression that wrap all the sequence.

The process is recursive, so we need to combine the first 2 expression into only
one, and continue the process until finish the list

-}
makeBinOpSeq :: Expr -> [(La.Operation, Expr)] -> Expr
makeBinOpSeq e1 [] = e1
makeBinOpSeq e1 ((op,e2):xs) = makeBinOpSeq (makeBinOp op e1 e2) xs


{- |
Takes a valid binary operator and its left and right operand expression and
returns the corresponding expression. It use association list `assocOpCons' to
associte the valid operator with the Expr constructors.
-}
makeBinOp :: La.Operation -> Constructor
makeBinOp op e1 e2 =
  case lookup op assocOpCons of
    Just c -> c e1 e2
    Nothing -> error ("Invalid operator " <> show op)
  where
    assocOpCons =
      [
        (La.Summatory, Add),
        (La.Difference, Sub),
        (La.Multiplication, Mul),
        (La.Division, Div)
      ]